E46 Coupe Front and Rear "Wheel Rates"

home

back to tech

E46 Coupe Front and Rear "Wheel Rates"

Parameters involved in determining rear wheel rate

Figure 1

Figure 1 shows the relevant parameters involved in calculating the wheel rate based on knowledge of the spring rate. Wheel rates are useful to know as they make it possible to compare rates between chassis' with differing suspension layouts. Wheel rate is also nice in that it gives one a better feel for the front to rear rates on a single car when the two axles have differing motion ratios (L1/L2, see below). It might be helpful to think of wheel rate as the effective spring rate when the spring is actually installed onto the car.

On the E46 Coupe chassis the rear swing arm is defined as the upper control arm. But the swing arm does not extend merely to the outer pivot point. It must ideally be defined to end at the center of the rear tire contact patch. Actual determination of the correct length to use for the swing arm is not trivial. Alternatively one can measure how far the two spring perches move together when the center of the rear tire is moved a certain distance. This gives us the motion ratio.

Spring rates are usually expressed as lbs/in. In other words, if we compress a given spring by one inch, how much resistance does it offer? If a spring that is compressed 1" pushes back with a force of 500 lbs than that spring is rated as 500 lbs/in (assuming it is linear).

What we want to do here is determine a similar type of rate for the wheel. How much force does it take to push the wheel up a distance of one inch? The force required will be equal to the "effective wheel rate". A torque balance on the swing arm will help us answer this question.

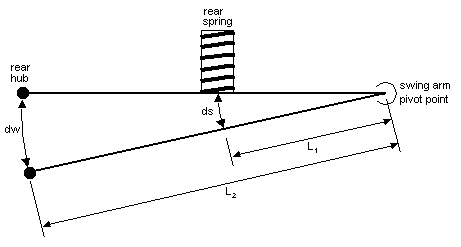
If we push up on the wheel and displace it by 1 inch (dw = 1" in Figure 1) - how far does this compress the spring (ds in Figure 1)? From similar triangles we calculate ds as:

L1/(ds) = L2/(dw) which leads to: ds = (L1/L2)dw

We will call the spring rate k1 (lbs/in). The force exerted on the wheel by the compressed spring is:

F1 = k1(ds) = k1(L1/L2)dw

Now use the moment balance on the swing arm to calculate F2:

F2 = (L1/L2)F1 = k1(L1/L2)²dw

Divide through by dw to yield the "wheel rate":

Wheel Rate = F2/dw = k1(L1/L2)²

Wheel Rate = Spring Rate x (Motion Ratio)²

NOTE the power of 2 on the motion ratio. The motion ratio must be squared when calculating wheel rate. This never fails to mess people up, as it easy to overlook unless you develop the equations as we did here.

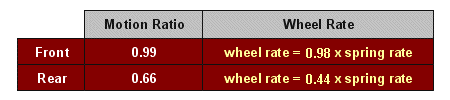
Summary of Results

For the E46 Coupe chassis we get the following table. If you know your spring rates then you can calculate your wheel rates using the yellow formulas. Note that the front wheel rate is just about equal to the spring rate. The motion ratios are obtained by calculating the slope of the curve of displacement of the center of the front and rear brake rotors vs. change in distance between spring perches.

home

back to tech